Challenge question #41 (04/01/2017)
Junior Question
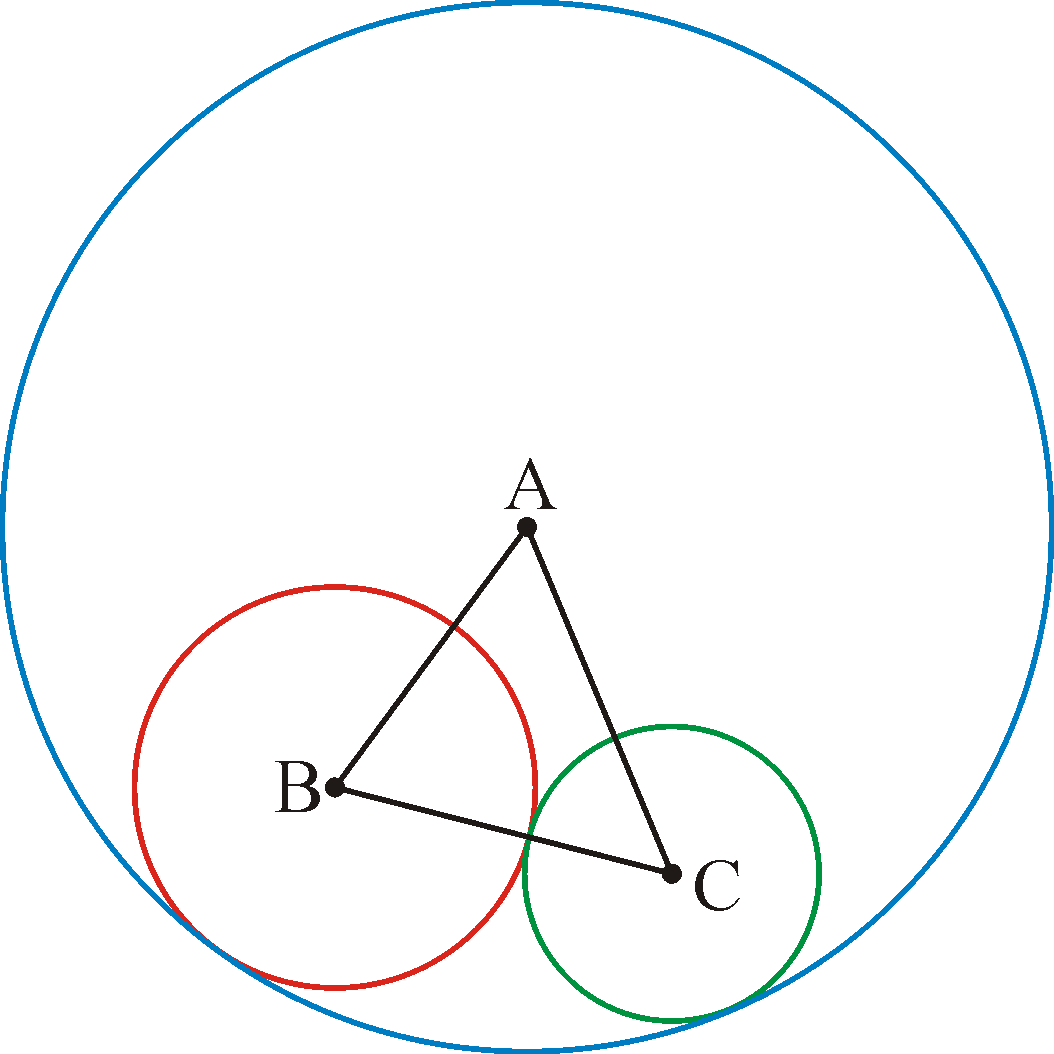Two circles with centres B and C touch each other externally, and touch a given fixed circle with centre A internally.
Show that as the two smaller circles vary in size, the perimeter of triangle ABC remains constant.
Senior Question
Show that by adding one to the product of four consecutive integers, a perfect square is obtained.
For example, $2\times$ $3\times$ $4\times$ $5+$ $1=$ $121=$ $11^{2}$
