Challenge question #46 (13/03/2017)
Junior Question
A fast food outlet sells chicken nuggets in packs of $4$ and $9$.
What is the largest number of nuggets that cannot be bought with a combination of these packs?
Senior Question
 O is a point inside the triangle ABC. Let K, L, and M be the mid-points of the sides [BC], [CA], [AB] respectively, and let X, Y, and Z be the midpoints of [OA], [OB], [OC] respectively.
O is a point inside the triangle ABC. Let K, L, and M be the mid-points of the sides [BC], [CA], [AB] respectively, and let X, Y, and Z be the midpoints of [OA], [OB], [OC] respectively.
Prove that the lines [KX], [LY], and [MZ] are concurrent.


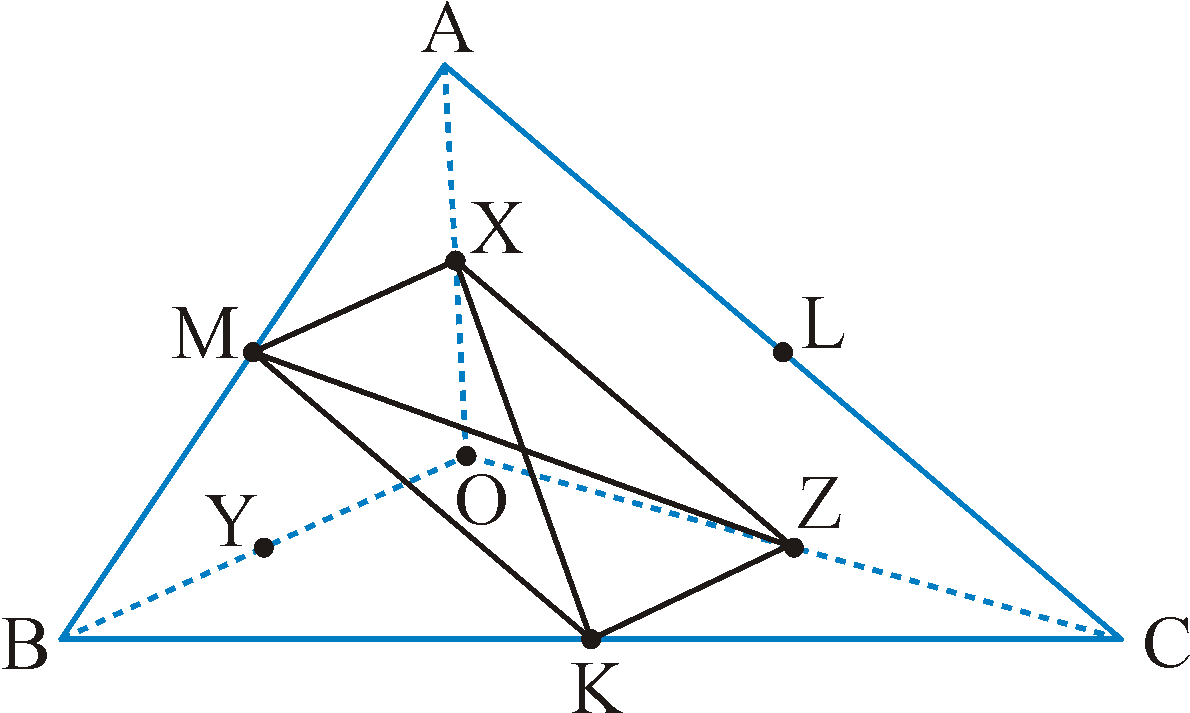 Join [XM], [MK], [KZ], and [ZX].
Join [XM], [MK], [KZ], and [ZX].


